(If you’re not one for preambles, you can skip to the puzzle.)

One of the greatest delights of my undergraduate career was attending Laci (rhymes with Yahtzee!) Babai’s combinatorics lectures. Often drawing affectionate comparisons with Count von Count from Sesame Street, Babai’s booming baritone and childlike enthusiasm have inspired legions of young students.

Coming from the Hungarian school, Babai’s mathematics focused on problem-solving, the untangling of knotty puzzles. Sometimes those puzzles were solved through the diligent application of standard techniques; sometimes linear algebra or another theoretical edifice and big-name theorem could be brought to bear; sometimes a whole kitchen sink of techniques, reductions, and case-work was necessary. But sometimes – just sometimes – there was an “Aha!” proof: a blinding flash of insight that instantly unraveled the knot and left the puzzle exposed and defenseless.

Laci cultivated reverence for the “Aha!” among his students, peppering his lectures with challenges that revealed their mysteries when viewed from that just-right angle, and often pausing to see whose eyes suddenly sparkled. His favorite puzzle involved a checkerboard, a pandemic, and an evil mastermind, and I’m going to lay it out for you here. But don’t worry: I will neither spoil the answer nor keep this gem permananently hidden. I recommend you try your best to divine an elegant, short, and utterly convincing argument. If, come what may, you either want to confirm your answer or simply must have it revealed, I’ve hidden the solution below, and I promise not to judge.

(Full disclosure: I spent a day with this problem and had to get a heavy-handed hint before seeing the solution. Meanwhile, some of my peers sniffed out the answer in under thirty seconds. Once you see it, you see it.)

(And also a disclaimer: The Aha! is but one beautiful and fun way of mathematizing. These types of arguments are not always available, and not always advisable. Over-cleverness sometimes obscures deeper structure.)

The Percolating Pandemic Puzzle

But without further ado, here is Babai’s puzzle: A pandemic has broken out on an $n\times n$ grid (think checkerboard, $n$ squares across and $n$ squares high). At time 0, some of the squares in the grid carry an infection. The infection then spreads according to the following rules:

1. Once infected, a square remains infected.
2. The infection spreads in discrete time steps where a previously uninfected square becomes infected if two or more of its edge-wise neighbors are infected.

As an example, here’s the infection spread on a $7\times 7$ board, with black indicating initially infected squares, and lighter shades corresponding to later infection times:

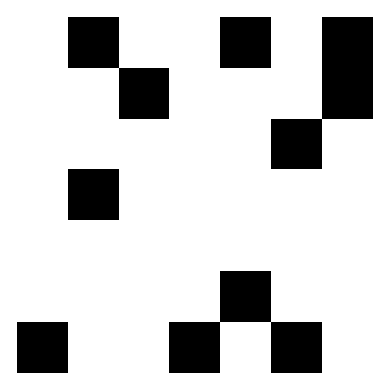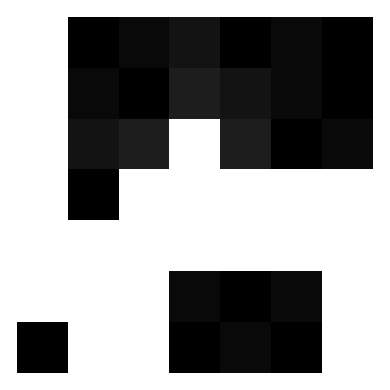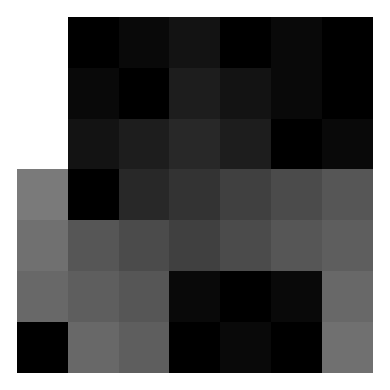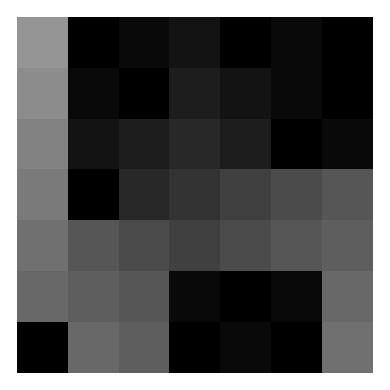
We now introduce the evil mastermind to the problem. Their goal is to infect the entire grid on a budget, so they want to determine the minimum number of (cleverly positioned) initially infected squares that lead to a fully infected grid. Some brief introspection reveals that $n$ initial infections along the diagonal of the square suffice (here pictured for $n=10$):

But the evil mastermind is greedy. Is it possible to do the job with fewer initially infected squares? That’s the puzzle! Stated more formally:

What is the minimal number of initially infected squares that can (when positioned in an optimal manner) lead to a full infection? Find this number and give an utterly convincing, very brief argument for why your answer is correct.

Good luck!

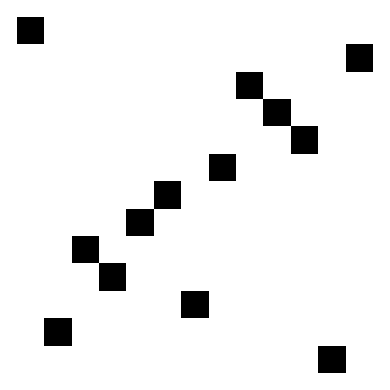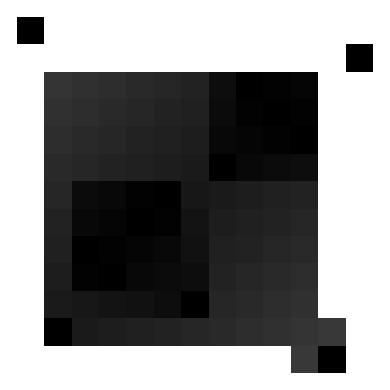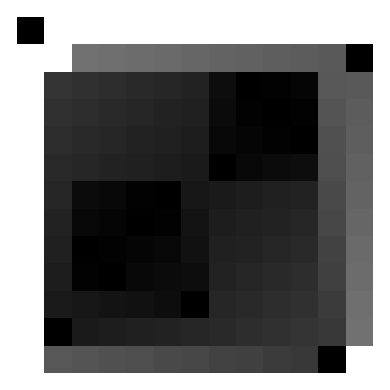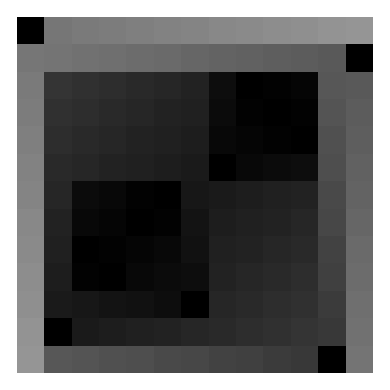
Now, I promised I wouldn’t leave you hanging but also wouldn’t give spoilers. Click on the arrows below to first reveal a hint (modest but substantive) and then reveal the solution. I’ve also included a followup puzzle in case you want to go deeper.

On a personal note, I was surprised to rediscover this problem when thinking about operads in equivariant homotopy theory for the work in this paper. Go figure!