I’m happy to announce two new preprints, the first with with Angélica Osorno and our students Usman Hafeez and Peter Marcus, and the second with Scott Balchin, Angélica, and Constanze Roitzheim:

• Saturated and linear isometric transfer systems for cyclic groups of order $p^mq^n$, arXiv:2109.08210.
• Model structures on finite total orders, arXiv:2109.07803.

Both of these build off of recent work Angélica and I did with another group of Reed students, Evan Franchere, Weihang Qin, and Riley Waugh:

• Self-duality of the lattice of transfer systems via weak factorization systems, arXiv:2102.04415, Homology, Homotopy and Applications.

These papers are about homotopy theory, either focused on transfer systems (related to $N_\infty$-operads in equivariant homotopy theory) or Quillen model structures (presentations of abstract homotopy theories on general categories). But our work is enumerative as well, and forms the basis of an initial foray into homotopical combinatorics – enumerative and structural descriptions of model (and related) structures on finite lattice posets.

In this post I want to describe our work in a fashion that will be particularly accessible to combinatorialists, stripping away the homotopical motivation (which you can find in the papers) in order to highlight some novel enumeration problems. I hope that some of my readers will be tempted to apply their expertise in this new arena!

Throughout, let’s fix a finite poset $P$ which is a lattice, meaning that it admits finite meets (greatest lower bounds, denoted $\wedge$) and finite joins (least upper bounds, denoted $\vee$). Such structures are ubiquitous in combinatorics, and examples include the finite total orders $[n] = {0 < 1 < \cdots < n}$ and subgroup lattices of finite groups.

The Hasse diagram for the Tamari lattice of full parenthesizations of five terms. Image: Wikipedia.

Transfer systems on lattices

A transfer system on a lattice $(P,\le)$ is a transitive relation $\to$ on $P$ that

• refines $\le$: $p\to q$ implies $p\le q$, and
• is closed under restriction: $p\to q$ and $r\le q$ implies $p\wedge r\to r$.

With an additional conjugation condition, these were introduced by equivariant homotopy theorists as relations on a subgroup lattice that encode compatible systems of multiplicative norms. Remarkably, they are in bijective correspondence with weak factorization systems on $P$ (see the next section).

Transfer systems on $[n]$

The transfer systems on $[n]$ were enumerated in this paper by Balchin, David Barnes, and Roitzheim, and they can be constructed recursively. Fix a transfer system $\to$ and let $k\in [n]$ be the smallest integer such that $k\to n$. Note that closure under restriction implies the relation $k\to \ell$ for all $\ell\ge k$. Diagrammatically, we can view the situation as follows:

The blue region is a transfer system on $[k]$, and the orange a transfer system on $[k+1,n]$. The curved arrows represent $k\to \ell$ for $\ell\ge k$. Image: BBR.

The restrictions of $\to$ to $[k-1]$ and to $[k+1,n]$ are both transfer systems, and given transfer systems on each of these, we can glue them together by taking their union and adding in $k\to \ell$ for $\ell\ge k$. After taking some care with the extremal cases $k=0,n$, we see that $T_n$, the number of transfer systems on $[n]$, satisfies the Catalan recurrence relation

with initial conditions $T_0=1$, $T_1=2$. As such, we have

where $\mathrm{Cat}(n)$ is the $n$-th Catalan number!

If you’re a combinatorialist reading this, then I am willing to wager you already love the Catalan numbers. If not, here are a couple of the things that $\mathrm{Cat}(n)$ enumerates:

• balanced strings of $2n$ parentheses,
• complete parenthesizations of $n+1$ factors,
• full binary trees with $n+1$ leaves,
• Dyck paths: east-north lattice paths from $(0,0)$ to $(n,n)$ on $[0,n]^2$ that never cross the diagonal,
• triangulations of a convex $(n+2)$-gon,
• noncrossing partitions of the set ${1,2,\ldots,n}$.

Stanley’s famous Exercise 6.19 from Enumerative Combinatorics, v.2 contains 66 structures enumerated by Catalan numbers, and an addendum contains many, many more.

Delightfully, homotopy theorists can now add to the list with transfer systems on $[n-1]$. Moreover, the set $T([n])$ of transfer systems on $[n]$ forms a lattice under refinement which is isomorphic to the Tamari lattice (see the Hasse diagram in the first figure), which is the 1-skeleton of the associahedron. (Here’s a shameless self-link to an article I wrote about the associahedron for Reed Magazine.) Something interesting is afoot.

Weak factorization systems on lattices

Surprisingly, transfer systems on lattices are in bijection with weak factorization systems, a type of object that arises in categorical homotopy theory. A weak factorization system on a lattice $(P,\le)$ is an ordered pair of relations $(L,R)$ each refining $\le$ satisfying

• factorization: if $p\le q$, then there exists $r$ such that $p~L~r~R~q$, and
• lifting: $L = {}^⧄ R$ and $R = L^⧄$ (notation to be explained shortly).

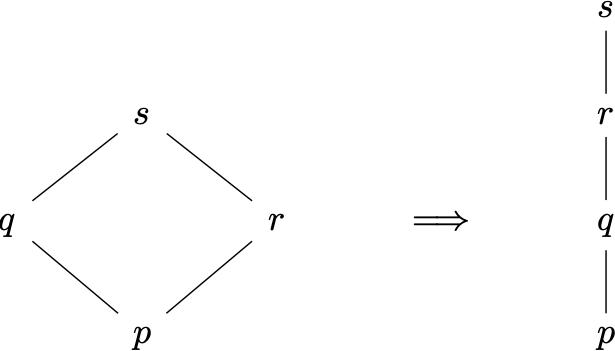
Here lifting is usually conceptualized in terms of commutative diagrams, but we can translate into posets: say that $p\le q$ has the left lifting property (LLP) with repsect to $r\le s$ when $p\le r$ and $q\le s$ implies that $q\le r$; in this situation, we also say that $r\le s$ has the right lifting property (RLP) with respect to $p\le q$.

Since this definition is crucial to all that follows, let’s take the time to unpack it a bit. Fix $p\le q$ and $r\le s$. In case either of $p\le r$, $q\le s$ is false, then we (vacuously) say that $p\le q$ has LLP with respect to $r\le s$. But when we have the “diamond” of relations $p\le q\le s$ and $p\le r\le s$, left lifting of $p\le q$ relative to $r\le s$ says that the diamond “straightens” into a chain: $p\le q\le r\le s$.

The substantive case of $p\le q$ having LLP with respect to $r\le s$. The diagram is drawn in “Hasse style” but the indicated inqualities need not be covering (i.e. minimal) relations.

Now given a relation $M$ refining $\le$ on $P$, we define

and

The bijection between transfer systems and weak factorization systems on lattices is quite simple. Notated somewhat glibly, it amounts to

In other words, we set $R = {\to}$ and – as we must – $L = {}^⧄R$.

One of the main results of Self-duality of the lattice of transfer systems via weak factorization systems is to establish this bijection and use it to show that transfer systems on a self-dual lattice also carry a duality.

Premodel structures on lattices

A compatible pair of weak factorization stystems is called a premodel structure. More prescisely, a premodel structure on a lattice $P$ consists of a pair of weak factorization systems \(\{(AC,F),(C,AF)\}\) for which $AF$ refines $F$ (equivalently, $AC$ refines $C$). We call $F$ the fibrations, $C$ the cofibrations, $AF$ the anodyne fibrations, and $AC$ the anodyne cofibrations. Reid Barton’s thesis is the go-to reference for premodel structures.

Since weak factorization systems correspond to transfer systems by taking right relations, this is the same data as having a pair of transfer systems, one refining the other. Transfer systems form a lattice under refinement, so in the language of posets, premodel structures on $P$ are the same thing as intervals (pairs $(x,y)$ with $x\le y$) in the lattice of transfer systems on $P$. Symbolically,

where $\mathrm{Pre}$ denotes premodel structures, and $\mathrm{Int}$ denotes intervals.

Premodel structures on $[n]$

Since $\mathrm{Tr}([n])$ is the Tamari lattice, we see that $\mathrm{Pre}([n])$ corresponds to intervals in the Tamari lattice. These were enumerated by Frédéric Chapoton in a 2006 paper. Tracking the indices carefully, we see that

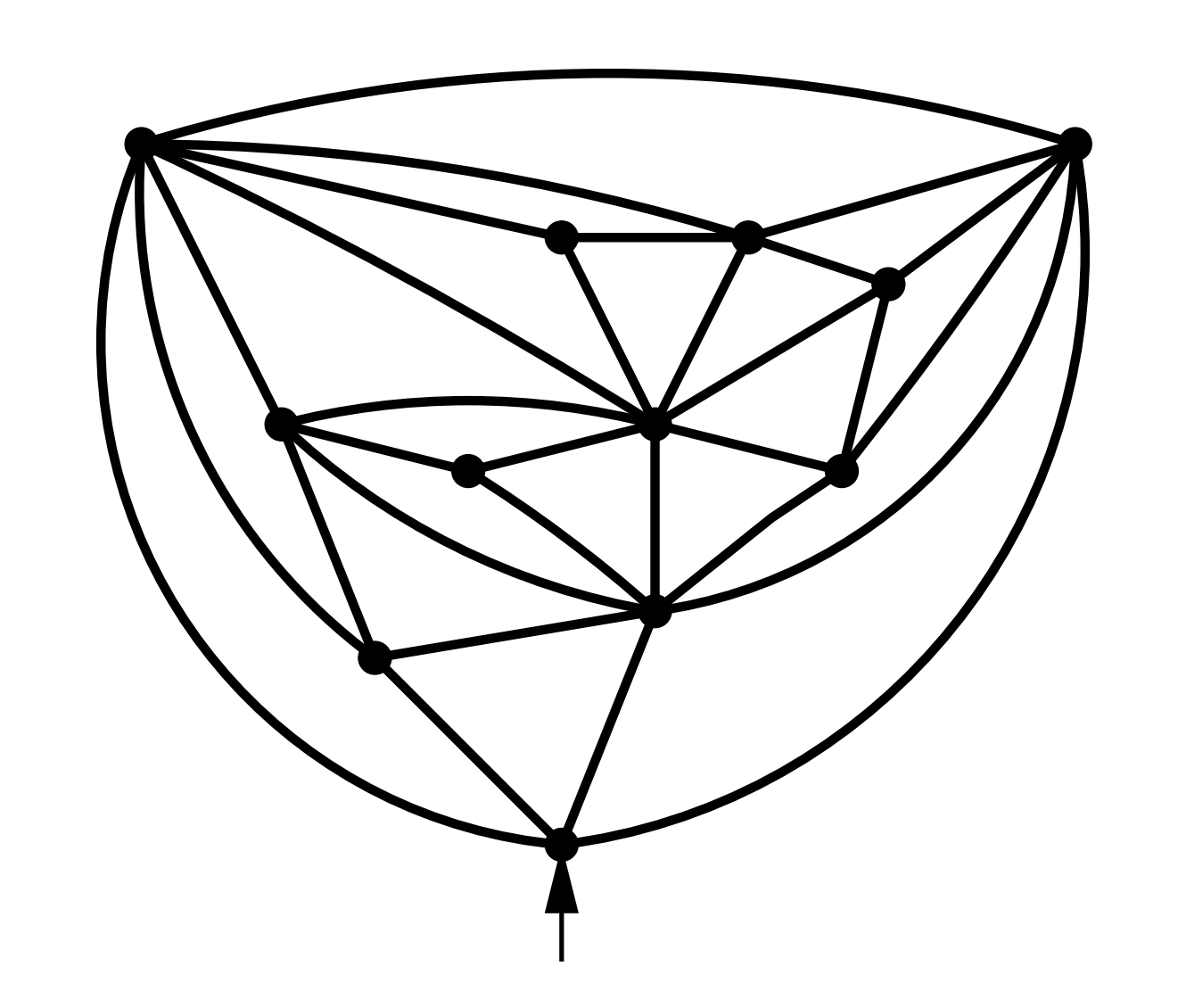
Fascinatingly, these numbers show up in other corners of mathematics. Indeed, Tutte showed that this is the number of triangulations (rooted planar graphs in which all faces have three vertices, up to continuous deformation) with $n+1$ internal vertices, and Bernardi and Bonichon produce an explicit bijection between Tamari intervals and such triangulations.

A triangulation with 9 internal vertices. Image: BB.

In principle, the Bernardi-Bonichon construction induces a bijection between premodel structures on $[n]$ and triangulations with $n+1$ internal vertices. We have not yet explored whether there is a reasonably explicit or pincipled description of this bijection that makes a conceptual link between these structures.

Model structures on lattices

We’re now ready for model structures. As the name indicates, these are premodel structures satisfying an additional condition:

• two-out-of-three: set \(W = AF\circ AC = \{p\le q\mid p~AF~r~AC~q\text{ for some }r\}\); if $p\le r\le q$ and two of $p~W~r$, $r~W~q$, $p~W~q$ hold, then so does the third.

The relation $W$ is called weak equivalence, and in homotopy theory it’s the star of the show: the job of a model structure is to give a nice way to turn the relations of $W$ into isomorphisms. In the case of model structures on lattices, the relation $W$ is automatically saturated:

• saturation (aka decomposition): if $p~W~q$ and $p\le r\le q$, then $p~W~r$ and $r~W~q$.

Given a model structure on a lattice $(P,\le)$, we may form the associated homotopy lattice $\mathrm{Ho}(P)$ which is the quotient of $P$ by the equivalence relation generated by $W$, endowed with the partial order induced by $\le$. Later, we will see that it can be interesting to enumerate model structures on $P$ with a particular homotopy lattice.

It turns out that there is a bijection between weak factorization systems and contractible model structures: those with $W = {\le}$ (or, equivalently, $\mathrm{Ho}(P)$ a singleton). The recipe is as follows: given a weak factorization system $(L,R)$, set $({AC}, F) = (C,{AF}) = (L,R)$. Note that $W = {AF}\circ {AC} = L\circ R = {\le}$ by the factorization property of $(L,R)$. This gives us a triple of bijections:

Bijections between transfer systems, weak factorization systems, and contractible model structures on $P$. Image: BOOR.

Model structures on $[n]$

When $P=[n]$, a straightforward but somewhat involved argument implies that a model structure on $[n]$ is specified by (and specifies) choices of contractible model structures on each connected component. (This is very special to $[n]$ and does not hold for other lattices!) Thus the following recipe uniquely identifies each model structure on $[n]$:

1. Choose a partition of $[n]$ into intervals,

   \[[n] = [0,a_1]\amalg [a_1+1,a_2]\amalg \cdots \amalg [a_k+1,n].\]

2. On each interval in the partition, choose a transfer system.

The interval $[a_j+1,a_{j+1}]$ is isomorphic to $[a_{j+1}-a_j-1]$ and thus there are $\mathrm{Cat}(a_{j+1}-a_j)$ transfer systems on it. (This works for the initial and final interval as well if we set $a_{-1}=-1$ and $a_{k+1} = n$.) Noting that an interval partition of $[n]$ (with $k+1$ blocks) is equivalent to an ordered partition (i.e., composition) of the integer $n+1$, we see that there are

model structures on $[n]$. Classical results of Shapiro imply that this number is the binomial coefficient

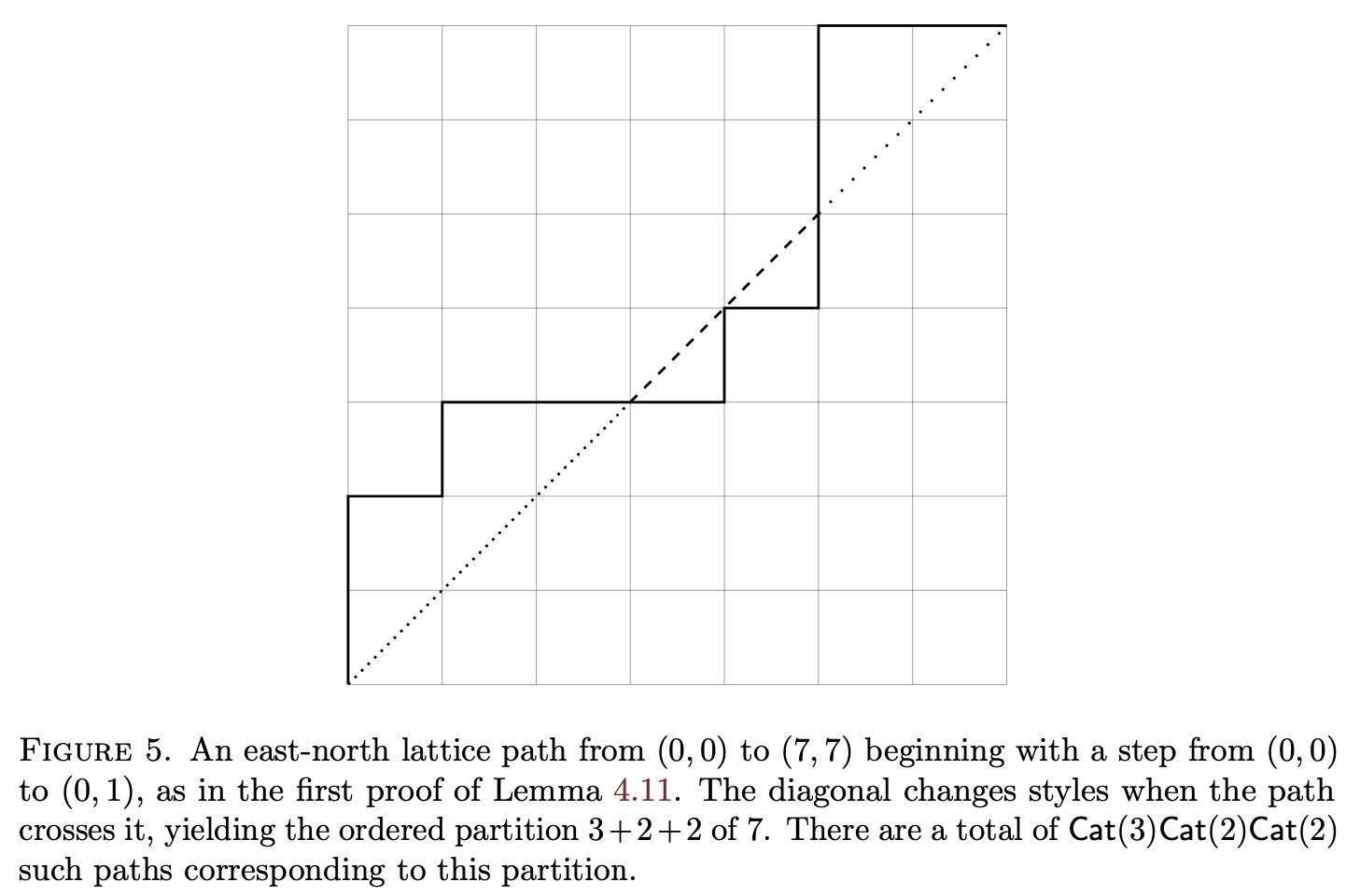
In fact, we give a new direct proof of this identity via lattice paths that the reader might deduce from this diagram:

An example of our bijective proof that equation (9) evaluates to (10). Image: BOOR.

The above recipe also allows us to enumerate model structures on $[n]$ with a specified homotopy category. Indeed, $\mathrm{Ho}([n])\cong [k]$ for $0\le k\le n$ precisely when there are $k+1$ blocks in the associated interval partition. As such (again by a theorem of Shapiro), there are

model structures on $[n]$ with $k+1$ connected components.

We can arrange these counts into Shapiro’s Catalan triangle (OEIS A039598), which has the Catalan numbers as its first column (corresponding to contractible model structures) and row sums giving the total number model structures on $[n]$.

This table gives the number of model structures on $[n]$ with homotopy category isomorphic to $[k]$. The rightmost column gives the total number of model structures on $[n]$. Image: BOOR.

Model structures on lattices with $F = {\le}$

The paper Saturated and linear isometric transfer systems for cyclic groups of order $p^mq^n$ focuses on so-called saturated transfer systems, where the relation satisfies the saturation condition. The interested reader can check that these are in bijection with model structures on $P$ for which $ F = {\le}$. Via techniques that probably deserve their own blog post, we show that the rectangular lattice $[m]\times [n]$ has precisely

such model structures, where \(\begin{Bmatrix}r\\ s\end{Bmatrix}\) is the Stirling number of the second kind enumerating $s$-block partitions of a set with cardinality $r$. Moreover, the exponential generating function for $s(m,n)$ takes the form

A general strategy

Given a lattice $P$, you can attempt the following steps to determine model structures on $P$:

1. Determine the structure of the lattice of transfer systems $\mathrm{Tr}(P)$ (equivalently, weak facotrizaiton systems) in $P$.
2. Enumerate the premodel structures on $P$ by determining the interval lattice of $\mathrm{Tr}(P)$.
3. Figure out which intervals on $\mathrm{Tr}(P)$ correspond to model structures.

A word of warning: very few premodel structures are model structures! In the case of $P=[n]$, the quotient of # premodel structures on $[n]$ over # model structures on $[n]$ grows like

as $n\to \infty$ where $c = \frac{243\sqrt{3/2}}{1024} \approx 0.291$ and $d = 3\log_2(3)-6 \approx -1.245$. This is nearly exponential decay, and the quotient approaches $0$ very quickly.

Und jetzt

We cover several additional topics in the papers (including analyses of duality on and Bousfield localization of model structures on $[n]$), but there is still much to explore. The final section of Model structures on finite total orders provides a list of open problems. I hope you’ll think about them and share your progress and questions!